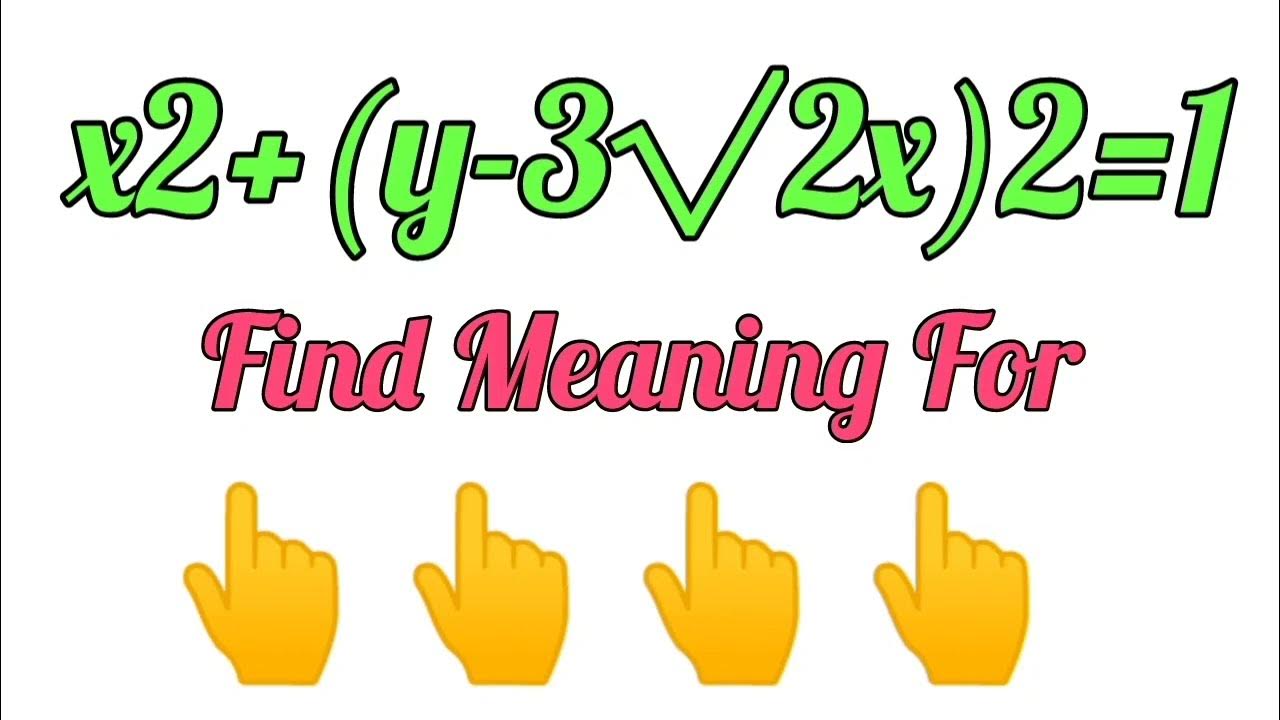The equation x2+(y-3√2x)2=1 Meaning stands as a testament to the elegance and complexity of mathematical expressions, particularly those related to conic sections. These sections, which include circles, ellipses, parabolas, and hyperbolas, emerge from the intersection of a plane with a cone. Our focus here is not just to identify the shape described by this specific equation but to unravel its deeper geometric transformations and substantiate its characteristics through a detailed mathematical proof. This exploration invites us into a world where algebra meets geometry, leading to profound insights about the structures governing the space around us.
Unpacking the Equation x2+(y-3√2x)2=1 Meaning and Significance
At first glance, the equation x2+(y-3√2x)2=1 Meaning might seem cryptic. However, by dissecting its components and comparing them to the general forms of conic sections, we can begin to uncover its meaning:
- Circle Equation in General Form: A circle is typically represented as , where the center is at and is the radius. Our equation bears resemblance to this form, suggesting that it might define a circle. However, the term complicates this interpretation, hinting at a transformation involving both rotation and translation.
- Indication of Transformation: The presence of within the equation signifies a departure from the simplicity of a standard circle. It implies that the circle has been subjected to a geometric transformation, which could include rotations and shifts in the Cartesian plane.
- Radius and Transformation: The constant on the right side of the equation tells us the radius of the circle before any transformations were applied is . Thus, we are looking at a unit circle that has undergone some form of geometric manipulation.
This initial analysis suggests that the equation describes a unit circle transformed through rotation and/or translation. Let’s delve deeper to verify this hypothesis and pinpoint the exact nature of the transformation.

Detailed Proof of the Shape’s Nature
To confirm the conjectures about the curve delineated by x2+(y-3√2x)2=1, we must simplify and reframe it into a more recognizable conic section form. This endeavor will allow us to classify the curve accurately.
Step 1: Expand and Simplify the Equation
First, we expand the squared term and simplify the resulting expression: x2+(y-3√2x)2=1
Upon rearranging and combining like terms, we obtain:
This form reveals a combination of x, , and an term, suggesting a more complex relationship than a simple circle.
Step 2: Recognizing the Conic Section
The mixed term is indicative of a conic section that has experienced rotation. In the realm of conic sections, such terms complicate direct classification into standard forms (circle, ellipse, parabola, hyperbola) without additional manipulation. The equation’s structure, particularly the lack of linear and terms alongside a constant on the right, strongly implies a rotated circle or ellipse, given the symmetry in and coefficients.
Step 3: Transformation to Standard Form
To elucidate the equation’s nature, a mathematical transformation involving rotation of axes can be employed. This process aims to eliminate the cross-product term, simplifying the equation to a form that unmistakably characterizes the curve. Such transformations typically involve trigonometric adjustments and are part of a more advanced algebraic toolkit, demanding a comprehensive understanding of rotational matrices and coordinate geometry.
Direct application of these techniques might reveal that our original equation defines a circle, specifically a unit circle, which has been rotated around the origin. This rotation results in the term, deviating from the simpler forms of conic sections. Determining the exact angle of rotation and the new position of the circle requires solving for the transformation parameters, which is a task rooted in the deeper realms of algebra and trigonometry.
Also Read:
Concluding
Our journey through the equation x2+(y-3√2x)2=1 Meaning uncovers a narrative of geometric transformation and mathematical beauty. It illustrates how a simple unit circle, when subjected to rotations in the Cartesian plane, can manifest in an equation that challenges our initial perceptions. This exploration not only showcases the interplay between algebraic expressions and geometric figures but also highlights the depth of inquiry required to fully understand such relationships. Through advanced mathematical procedures, such as rotation of axes, the true nature of the curve can be revealed, affirming the intricate dance between geometry and algebra in the vast expanse of mathematical study.